ابزارآلات کنترلی

هفت ابزار اصلی کیفیت عبارت است از تعیین مجموعه ای از تکنیک های گرافیکی که در عیب یابی مشکلات مربوط به کیفیت مفیدترین است. به دلیل اینکه برای افرادی که آموزش رسمی کمی در زمینه آمار دارند مناسب است و می توان از آنها برای حل اکثریت مسائل مربوط به کیفیت استفاده کرد ، اصطلاحاً اساسی نامیده می شود.
این هفت ابزار عبارتند از:

نمودار علت و معلولی (همچنین به عنوان “نمودار استخوان ماهی” یا نمودار ایشیکاوا شناخته می شود)

• برگه چک 
• نمودار کنترلی
• هیستوگرام
• نمودار پارتو
• نمودار پراکندگی
• طبقه بندی (متناوبا ، نمودار جریان یا نمودار اجرا)

این نامگذاری در ژاپن پس از جنگ با الهام از هفت سلاح معروف بنکی به وجود آمد. این احتمالاً توسط Kaoru Ishikawa معرفی شد که به نوبه خود تحت تأثیر مجموعه ای از سخنرانی های W. Edvard Deming در سال ۱۹۵۰ برای مهندسان و دانشمندان ژاپنی بود. در آن زمان ، شرکتهایی که برای آموزش نیروی کار خود در زمینه کنترل کیفیت آماری اقدام کرده بودند.

دریافتند که پیچیدگی موضوع اکثر کارگران آنها را مرعوب می کند و آموزش را متوقف می کند تا در درجه اول روی روشهای ساده تر تمرکز کنند که برای اکثر مسائل مربوط به کیفیت کافی است. موسسه مدیریت پروژه هفت ابزار اساسی در راهنمای مجموعه مدیریت پروژه را به عنوان نمونه ای از مجموعه ابزارهای عمومی مفید برای برنامه ریزی یا کنترل کیفیت پروژه ارجاع می دهد.

هفت ابزار اساسی در مقابل روشهای آماری پیشرفته تر مانند نمونه گیری پیمایشی ، نمونه گیری پذیرش ، آزمایش فرضیه های آماری ، طراحی آزمایشها ، تجزیه و تحلیل چند متغیره و روشهای مختلف توسعه یافته در زمینه تحقیقات عملیاتی قرار دارند.

نمودار ایشیکاوا

نمودارهای ایشیکاوا (که نمودارهای استخوان ماهی ، نمودارهای ماهیان ، نمودارهای علت و معلولی یا فیشیکاوا نیز نامیده می شوند) نمودارهای علی هستند که توسط Kaoru Ishikawa ایجاد شده اند و علل بالقوه یک رویداد خاص را نشان می دهند.

کاربردهای رایج نمودار Ishikawa طراحی محصول و جلوگیری از نقص با کیفیت برای شناسایی عوامل بالقوه ایجاد کننده اثر کلی است. هر علت یا دلیلی برای نقص منبع تنوع است. معمولاً علل به منظور طبقه بندی و طبقه بندی این منابع تنوع به دسته های اصلی گروه بندی می شوند.

بررسی اجمالی

این نقص به عنوان سر ماهی ، رو به راست نشان داده می شود و علل آن به سمت چپ به عنوان استخوان ماهی گسترش می یابد. دنده ها به دلایل عمده از ستون فقرات منشعب می شوند ، و برای دلایل ریشه ، شاخه های فرعی ، تا میزان مورد نیاز.

نمودارهای ایشیکاوا در ۱۹۶۰s توسط Kaoru Ishikawa ، که پیشگام فرایندهای مدیریت کیفیت در کارخانه های کشتی سازی کاوازاکی بود ، رواج یافت و در این فرآیند به یکی از بنیانگذاران مدیریت مدرن تبدیل شد.

مفهوم اساسی برای اولین بار در دهه ۱۹۲۰ مورد استفاده قرار گرفت و یکی از هفت ابزار اساسی کنترل کیفیت محسوب می شود. به دلیل شکل آن ، شبیه به نمای جانبی اسکلت ماهی ، به عنوان نمودار استخوان ماهی شناخته می شود.

مزدا موتورز از یک نمودار Ishikawa در توسعه ماشین اسپرت Miata (MX5) استفاده کرد.

مزایای

ابزار طوفان فکری بسیار بصری که می تواند نمونه های بیشتری از دلایل اصلی را جرقه بزند
به سرعت تشخیص دهید که آیا علت اصلی چندین بار در یک درخت علّی یکسان یا متفاوت یافت شده است
به فرد اجازه می دهد همه علل را به طور همزمان مشاهده کند
تجسم خوب برای ارائه مسائل به ذینفعان

معایب

نقص های پیچیده ممکن است دلایل زیادی ایجاد کنند که ممکن است از نظر بصری به هم ریخته شود
روابط متقابل بین علل به راحتی قابل تشخیص نیست
علل ریشه ای
تجزیه و تحلیل علل ریشه ای برای نشان دادن روابط کلیدی بین متغیرهای مختلف در نظر گرفته شده است و علل احتمالی بینش بیشتری در مورد رفتار فرایند ارائه می دهد.

علل با تجزیه و تحلیل اغلب از طریق جلسات طوفان مغزی نمایان می شوند و در شاخه های اصلی استخوان ماهی در دسته بندی می شوند. برای کمک به ساختار رویکرد ، دسته بندی ها اغلب از یکی از مدل های رایج زیر نشان داده می شوند ، اما ممکن است به عنوان یک مورد منحصر به فرد برای برنامه در یک مورد خاص ظاهر شوند.

هر علت بالقوه ای برای یافتن علت اصلی ، اغلب با استفاده از تکنیک ۵ چرا ردیابی می شود.

دسته های معمولی عبارتند از:

۵ Ms (مورد استفاده در تولید)

همچنین ببینید: مدل ۵M
۵ Ms که از تولید ناب و سیستم تولید تویوتا سرچشمه می گیرد ، یکی از رایج ترین چارچوب ها برای تجزیه و تحلیل علت اصلی است:

• نیروی انسانی / قدرت ذهن (کار فیزیکی یا دانش ، شامل: قایزها ، پیشنهادات)
• ماشین (تجهیزات ، فناوری)
• مواد (شامل مواد اولیه ، مواد مصرفی و اطلاعات)
• روش (فرایند)
• اندازه گیری / متوسط ​​(بازرسی ، محیط)

این موارد توسط برخی گسترش یافته و شامل سه مورد دیگر می شود و به آنها ۸ Ms گفته می شود:

• ماموریت / طبیعت مادر (هدف ، محیط)
• مدیریت / قدرت پول (رهبری)
• نگهداری
• ۸ Ps (مورد استفاده در بازاریابی محصول)

همچنین ببینید: آمیخته بازاریابی
این مدل رایج برای شناسایی ویژگیهای مهم برای برنامه ریزی در بازاریابی محصول اغلب در تجزیه و تحلیل ریشه ای به عنوان دسته هایی برای نمودار Ishikawa استفاده می شود:

• محصول (یا خدمات)
• قیمت
• محل
• ترویج
• افراد (پرسنل)
• روند
• شواهد فیزیکی (اثبات)
• کارایی
• ۸ Ps در درجه اول در بازاریابی محصول استفاده می شود.

۴ S (مورد استفاده در صنایع خدمات)
جایگزینی که برای صنایع خدماتی استفاده می شود ، از چهار دسته علت احتمالی استفاده می کند:

• محیط اطراف
• تامین کنندگان
• سیستم های
• مهارت

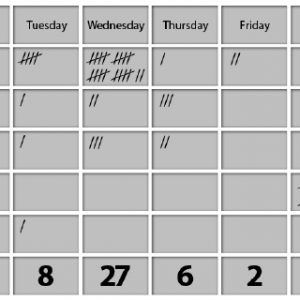
Check sheet

برگه چک یک فرم (سند) است که برای جمع آوری داده ها در زمان واقعی در مکانی که داده ها تولید می شوند استفاده می شود. داده های ضبط شده می تواند کمی یا کیفی باشد. وقتی اطلاعات کمی است ، چک برگه را گاهی اوقات یک برگه شمارش می نامند.

برگه چک یکی از اصطلاحاً هفت ابزار اساسی کنترل کیفیت است.

قالب بندی

ویژگی بارز یک برگه چک این است که داده ها با ایجاد علائم (“چک”) روی آن ثبت می شوند. یک برگه چک معمولی به مناطق تقسیم می شود و علائم ایجاد شده در مناطق مختلف اهمیت متفاوتی دارند. داده ها با رعایت مکان و تعداد علائم روی برگه خوانده می شوند.

برگه های چک معمولاً از عنوانی استفاده می کنند که به پنج W پاسخ می دهد:

• چه کسی برگه چک را پر کرد
• آنچه جمع آوری شد (هر چک چه چیزی را نشان می دهد ، یک دسته شناسایی یا شماره قطعه)
• محل جمع آوری (امکانات ، اتاق ، دستگاه)
• زمان جمع آوری (ساعت ، شیفت ، روز هفته)
• چرا داده ها جمع آوری شده است.

عملکرد

Kaoru Ishikawa پنج مورد را برای برگه های چک در کنترل کیفیت مشخص کرد

• برای بررسی شکل توزیع احتمال یک فرایند
• برای تعیین کمبودها بر اساس نوع
• برای تعیین کمبود نقص ها بر اساس مکان
• برای تعیین کمبودهای ناشی از علت (ماشین ، کارگر)
• برای پیگیری تکمیل مراحل در یک روش چند مرحله ای (به عبارت دیگر ، به عنوان یک چک لیست)
• برای ارزیابی شکل توزیع احتمال یک فرایند

هنگام ارزیابی توزیع احتمال یک فرایند ، می توان تمام داده های پردازش را ثبت کرد و سپس منتظر ماند تا توزیع فرکانس در زمان بعدی ایجاد شود. با این حال ، از یک برگه چک می توان برای ایجاد توزیع فرکانس در حین مشاهده روند استفاده کرد.

این نوع برگه چک شامل موارد زیر است:

• شبکه ای که ضبط می کند
• هیستوگرام در یک بعد قرار می گیرد
• تعداد یا فراوانی مشاهدات فرآیند در سطل مربوطه در بعد دیگر
• خطوطی که محدوده مشخصات بالا و پایین را مشخص می کنند
• توجه داشته باشید که افراط در مشاهدات فرآیند باید قبل از ساختن برگه چک به طور دقیق پیش بینی شود.

هنگامی که توزیع فرآیند آماده ارزیابی است ، ارزیاب عنوان برگه چک را پر می کند و به طور فعال روند را مشاهده می کند. هر بار که فرآیند خروجی تولید می کند ، خروجی را اندازه گیری می کند (یا در غیر این صورت ارزیابی می کند) ، سطل زنجیری که اندازه گیری در آن قرار دارد را تعیین می کند و به علامت های چک آن سطل اضافه می کند.

هنگامی که دوره مشاهده به پایان رسید ، ارزیاب باید آن را به شرح زیر بررسی کند:

آیا علامت های چک منحنی زنگ را تشکیل می دهند؟ آیا ارزشها منحرف هستند؟ آیا بیش از یک قله وجود دارد؟ آیا دور افتاده وجود دارد؟
آیا علامت های چک به طور کامل در محدوده مشخصات قرار می گیرند و جای خالی دارند؟ یا تعداد قابل توجهی علامت چک خارج از محدوده مشخصات وجود دارد؟
اگر شواهدی مبنی بر غیر عادی بودن وجود داشته باشد یا اگر فرآیند خروجی قابل توجهی را در نزدیکی یا فراتر از محدوده مشخصات تولید می کند ، باید تلاش برای بهبود فرایند برای حذف تنوع علت خاص انجام شود.

برای نوع نقص

وقتی فرآیندی به عنوان کاندیدای بهبود شناخته می شود ، مهم است که بدانید چه نوع نقصی در خروجی ها و فرکانس های نسبی آنها رخ می دهد. این اطلاعات به عنوان راهنمایی برای بررسی و حذف منابع نقص ، با شروع بیشترین موارد ، عمل می کند.

این نوع برگه چک شامل موارد زیر است:

یک ستون واحد که هر دسته نقص را فهرست می کند
یک یا چند ستون که مشاهدات مربوط به ماشین ها ، مواد ، روشها و اپراتورهای مختلف باید در آنها ثبت شود
توجه داشته باشید که مقوله های نقص و نحوه قرار دادن خروجی های فرآیند در این دسته ها باید قبل از ساختن برگ چک مورد توافق قرار گرفته و بیان شود. علاوه بر این ، قوانین ثبت عیوب انواع مختلف هنگامی که برای خروجی یکسان فرآیند مشاهده می شود ، باید وضع شود.

هنگامی که توزیع فرآیند آماده ارزیابی است ، ارزیاب عنوان برگه چک را پر می کند و به طور فعال روند را مشاهده می کند. هر بار که فرآیند خروجی تولید می کند ، خروجی نقص ها را با استفاده از روش های مورد توافق ارزیابی می کند ، دسته ای را که نقص در آن قرار دارد تعیین می کند و به علامت های چک آن دسته اضافه می کند. اگر هیچ نقصی برای خروجی فرآیند یافت نشد ، علامت چک ایجاد نمی شود.

پس از پایان دوره مشاهده ، ارزیاب باید از داده های بدست آمده نمودار پارتو تهیه کند. این نمودار سپس ترتیب بررسی فرایند و منابع تنوع را که منجر به برطرف شدن عیوب می شود ، تعیین می کند.

برای محل نقص

هنگامی که خروجی های فرآیند اجسامی هستند که ممکن است نقایص آنها در مکان های مختلف مشاهده شود (برای مثال حباب در محصولات چند لایه یا حفره های ریخته گری) ، نمودار غلظت نقص بسیار ارزشمند است.توجه داشته باشید که در حالی که اکثر انواع ورق ها مشاهدات بسیاری از فرآیندها را تجمیع می کنند خروجی ها ، معمولاً از یک برگه بررسی محل نقص در هر خروجی فرایند استفاده می شود.

این نوع برگه چک شامل موارد زیر است:

نمودار مقیاس شی از هر یک از طرفین آن ، به صورت اختیاری به بخشهای مساوی تقسیم می شود
هنگامی که توزیع فرآیند آماده ارزیابی است ، ارزیاب عنوان برگه چک را پر می کند و به طور فعال روند را مشاهده می کند. هر بار که فرآیند خروجی تولید می کند ، خروجی را برای نقص ها ارزیابی می کند و قسمتی از هر نمای را که هر کدام در آن یافت می شود علامت گذاری می کند. اگر هیچ نقصی برای خروجی فرآیند یافت نشد ، علامت چک ایجاد نمی شود.

هنگامی که دوره مشاهده به پایان رسید ، ارزیاب باید هر برگ چک را مجدداً بررسی کرده و ترکیبی از نقاط نقص را تشکیل دهد. استفاده از دانش وی در مورد فرآیند همراه با مکان ها باید منبع یا منابع تنوع ایجاد کننده نقص ها را آشکار کند.

به علت نقص

هنگامی که فرآیندی به عنوان کاندیدای بهبود شناخته می شود ، ممکن است به تلاش برای شناسایی منبع نقص ها به علت نیاز باشد.

این نوع برگه چک شامل موارد زیر است:

یک یا چند ستون که هر علت مشکوک را فهرست می کند (برای مثال ماشین ، مواد ، روش ، محیط ، اپراتور)
یک یا چند ستون که دوره ای را که در طی آن خروجی های فرایند باید مشاهده شوند (برای مثال ساعت ، شیفت ، روز) ذکر می کند.
یک یا چند نماد برای نشان دادن انواع مختلف عیوب که باید ثبت شوند – این نمادها جای علامت های چک سایر انواع نمودارها را می گیرند.
توجه داشته باشید که مقوله های نقص و نحوه قرار دادن خروجی های فرآیند در این دسته ها باید قبل از ساختن برگ چک مورد توافق قرار گرفته و بیان شود. علاوه بر این ، قوانین ثبت عیوب انواع مختلف هنگامی که برای خروجی یکسان فرآیند مشاهده می شود ، باید وضع شود.
وقتی توزیع فرآیند آماده ارزیابی شود ، ارزیابی کننده عنوان برگه چک را پر می کند. برای هر ترکیبی از علل مشکوک ، ارزیاب به طور فعال روند را مشاهده می کند. هر بار که فرآیند خروجی تولید می کند ، خروجی نقص ها را با استفاده از روش های مورد توافق ارزیابی می کند ، دسته ای را که نقص در آن قرار می گیرد تعیین می کند و نماد مربوط به آن دسته نقص را به سلول موجود در شبکه مربوط به شبکه اضافه می کند. ترکیبی از علل مشکوک اگر عیبی برای خروجی فرآیند یافت نشد ، نمادی وارد نمی شود.

هنگامی که دوره مشاهده به پایان می رسد ، ترکیب علل مشکوک با بیشترین نمادها باید برای منابع تنوع که نقایص نوع ذکر شده را ایجاد می کنند بررسی شود.

در صورت تمایل ، نمودار علت و معلولی ممکن است برای ارائه تشخیص مشابه استفاده شود. هنگام ارزیابی نقص ، ارزیاب به سادگی یک علامت چک در کنار “شاخه” در شاخه نمودار مربوط به علت مشکوک قرار می دهد.

چک لیست

در حالی که برگه های چک مورد بحث در بالا همه برای ضبط و دسته بندی مشاهدات است ، چک لیست به عنوان کمک کننده ای برای رفع اشتباه هنگام انجام مراحل چند مرحله ای ، به ویژه در هنگام بررسی و اتمام خروجی های فرآیند ، در نظر گرفته شده است.

این نوع برگه چک شامل موارد زیر است:

یک طرح کلی (اختیاری شماره گذاری شده) از خرده وظایف انجام شده
کادرها یا فضاهایی که ممکن است علامت های چک در آنها وارد شود تا زمان تکمیل فرعی را مشخص کند
یادداشت ها باید به ترتیب تکمیل شدن خرده وظایف انجام شوند.

انواع دیگر

برگه های چک محدود به موارد ذکر شده در بالا نیست. کاربران باید از تخیلات خود برای طراحی برگه های چک متناسب با شرایط استفاده کنند.

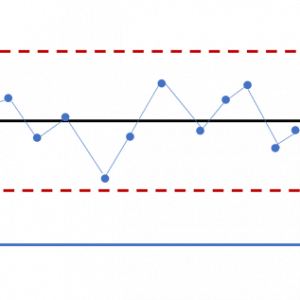
Control chart

نمودارهای کنترلی ، همچنین به عنوان نمودارهای Shewhart (پس از والتر A. Shewhart) یا نمودارهای فرآیند رفتار شناخته می شوند ، یک ابزار کنترل فرآیند آماری هستند که برای تعیین اینکه آیا یک فرآیند تولید یا تجارت در حالت کنترل است ، استفاده می شود. بهتر است بگوییم که نمودارهای کنترل دستگاه گرافیکی مانیتورینگ فرایندهای آماری (SPM) هستند. نمودارهای کنترلی معمولاً برای نظارت بر پارامترهای فرآیند هنگامی که شکل زیر توزیع فرآیند شناخته شده است ، طراحی می شوند. با این حال ، تکنیک های پیشرفته تری در قرن ۲۱ در دسترس است که در آن جریان داده های ورودی حتی بدون هیچ گونه آگاهی از توزیع فرآیند اساسی قابل نظارت است. نمودارهای کنترل بدون توزیع به طور فزاینده ای محبوب می شوند.

بررسی اجمالی

اگر تجزیه و تحلیل نمودار کنترل نشان می دهد که فرایند در حال حاضر تحت کنترل است (یعنی پایدار است ، و تنوع فقط از منابع مشترک در فرآیند ناشی می شود) ، هیچ اصلاح یا تغییری در پارامترهای کنترل فرآیند مورد نیاز یا مطلوب نیست. علاوه بر این ، داده های حاصل از فرآیند می تواند برای پیش بینی عملکرد آینده فرآیند مورد استفاده قرار گیرد. اگر نمودار نشان می دهد که فرآیند تحت نظارت کنترل نشده است ، تجزیه و تحلیل نمودار می تواند به تعیین منابع تنوع کمک کند ، زیرا این امر باعث کاهش عملکرد فرایند می شود.

فرآیندی که پایدار است اما خارج از محدوده دلخواه (مشخصات) عمل می کند (به عنوان مثال ، نرخ ضایعات ممکن است در کنترل آماری باشد اما بالاتر از محدوده مورد نظر است) باید با تلاش عمدی برای درک علل عملکرد فعلی و بهبود اساسی فرایند بهبود یابد.

نمودار کنترل یکی از هفت ابزار اساسی کنترل کیفیت است.معمولاً نمودارهای کنترلی برای داده های سری زمانی استفاده می شوند ، اگرچه می توان از آنها برای داده هایی استفاده کرد که قابلیت مقایسه منطقی دارند (یعنی می خواهید نمونه هایی را که همزمان گرفته شده اند یا عملکرد افراد مختلف را مقایسه کنید). اما نوع نمودار مورد استفاده برای این کار نیاز به توجه دارد.

تاریخ

نمودار کنترل توسط Walter A. Shewhart که در دهه ۱۹۲۰ در آزمایشگاه های بل کار می کرد ، اختراع شد. مهندسان این شرکت به دنبال بهبود قابلیت اطمینان سیستم های انتقال تلفن خود بودند. از آنجا که تقویت کننده ها و سایر تجهیزات باید در زیر زمین دفن می شدند ، نیاز به مشاغل قوی تری برای کاهش دفعات خرابی و تعمیرات وجود داشت. تا سال ۱۹۲۰ ، مهندسان به اهمیت کاهش تنوع در یک فرآیند تولید پی برده بودند. علاوه بر این ، آنها متوجه شده بودند که تنظیم مداوم فرایند در واکنش به عدم انطباق ، در واقع تنوع را افزایش می دهد و کیفیت را کاهش می دهد.

شوهرت مشکل را از نظر علل متداول و ویژه تنوع بیان کرد و در ۱۶ مه ۱۹۲۴ ، یک یادداشت داخلی نوشت و نمودار کنترل را به عنوان ابزاری برای تشخیص این دو معرفی کرد. رئیس شوهرت ، جورج ادواردز ، یادآور شد: “دکتر شوارت یک یادداشت کوچک فقط در مورد یک صفحه تهیه کرد. حدود یک سوم آن صفحه به یک نمودار ساده داده شد که امروزه همه ما آن را به عنوان یک نمودار کنترلی شماتیک می شناسیم. و متن کوتاهی که قبل و بعد از آن آمده بود ، همه اصول و ملاحظات اساسی را که در آنچه امروزه ما به عنوان کنترل کیفیت فرآیند می شناسیم ، شامل می شود. “شوارت تأکید کرد که آوردن یک فرآیند تولید به حالت کنترل آماری ، جایی که فقط تنوع علت مشترک وجود داشته باشد و کنترل آن برای پیش بینی خروجی آینده و مدیریت اقتصادی یک فرایند ضروری است.

شوارت با آزمایش های دقیق طراحی شده ، اساس نمودار کنترل و مفهوم وضعیت کنترل آماری را ایجاد کرد. در حالی که شوارت از نظریه های آماری محض ریاضی استفاده می کرد ، متوجه شد که داده های حاصل از فرایندهای فیزیکی به طور معمول “منحنی توزیع عادی” (توزیع گوسی ، که معمولاً “منحنی زنگ” نیز نامیده می شود) تولید می کند.

او کشف کرد که تغییرات مشاهده شده در داده های تولید همیشه مانند داده های موجود در طبیعت (حرکت براونی ذرات) عمل نمی کند. شوارت به این نتیجه رسید که در حالی که هر فرآیند تنوع را نشان می دهد ، برخی از فرایندها تنوع کنترل شده ای را نشان می دهند که برای روند طبیعی است ، در حالی که برخی دیگر تنوع کنترل نشده ای را نشان می دهند که در سیستم علتی فرایند در همه زمان ها وجود ندارد.
در سال ۱۹۲۴ یا ۱۹۲۵ ، نوآوری شوارت مورد توجه دبلیو ادواردز دمینگ قرار گرفت که در آن زمان در تاسیسات هاثورن کار می کرد.

دمینگ بعداً در وزارت کشاورزی ایالات متحده کار کرد و مشاور ریاضی اداره سرشماری ایالات متحده شد. در نیم قرن آینده ، دمینگ به عنوان اولین قهرمان و حامی کارهای شوارت تبدیل شد. پس از شکست ژاپن در پایان جنگ جهانی دوم ، دمینگ به عنوان مشاور آماری فرمانده عالی برای نیروهای متفق خدمت کرد. مشارکت بعدی وی در زندگی ژاپنی ها و حرفه طولانی وی به عنوان مشاور صنعتی در آنجا ، تفکر شوارت و استفاده از نمودار کنترلی را به طور گسترده در صنعت تولید ژاپن در دهه های ۱۹۵۰ و ۱۹۶۰ گسترش داد.

جزئیات نمودار

 

نمودار کنترل شامل موارد زیر است:

نقاط نشان دهنده آمار (به عنوان مثال ، میانگین ، محدوده ، نسبت) اندازه گیری ویژگی های کیفی در نمونه های گرفته شده از فرآیند در زمان های مختلف (به عنوان مثال ، داده ها)
میانگین این آمار با استفاده از همه نمونه ها محاسبه می شود (به عنوان مثال ، میانگین میانگین ، میانگین محدوده ها ، میانگین نسبت ها) – یا برای یک دوره مرجع که می توان تغییرات را در آن ارزیابی کرد. به طور مشابه می توان از میانه به جای آن استفاده کرد.
یک خط مرکزی به مقدار میانگین یا میانه آمار آماری ترسیم می شود
انحراف استاندارد (به عنوان مثال ، sqrt (واریانس) میانگین) آمار با استفاده از تمام نمونه ها محاسبه می شود – یا دوباره برای یک دوره مرجع که می توان تغییرات را در آن ارزیابی کرد. در مورد نمودارهای XmR ، دقیقاً تقریبی از انحراف استاندارد است ، فرض همگنی فرایند در طول زمان که انحراف استاندارد ایجاد می کند ، فرض نمی شود.
محدودیت های کنترل بالا و پایین (گاهی اوقات “محدودیت های فرایند طبیعی”) نامیده می شود که آستانه ای را نشان می دهد که در آن خروجی فرآیند از نظر آماری “بعید” تلقی می شود و معمولاً با ۳ انحراف استاندارد از خط مرکزی ترسیم می شود.

نمودار ممکن است دارای ویژگی های اختیاری دیگری باشد ، از جمله:

محدوده های هشدار یا کنترل بالا و پایین ، که به صورت خطوط جداگانه ترسیم شده اند ، معمولاً دو انحراف استاندارد در بالا و پایین خط مرکزی
تقسیم به مناطق ، با اضافه شدن قوانین حاکم بر فرکانس مشاهدات در هر منطقه
حاشیه نویسی با رویدادهای مورد علاقه ، که توسط مهندس کیفیت مسئول کیفیت فرآیند تعیین شده است
اقدام بر علل خاص
(n.b.، چندین مجموعه قانون برای تشخیص سیگنال وجود دارد ؛ این فقط یک مجموعه است. مجموعه قوانین باید به وضوح بیان شود.)

• هر نقطه خارج از محدوده کنترل
• اجرای ۷ نقطه در بالا یا همه زیر خط مرکزی – تولید را متوقف کنید
• قرنطینه و ۱۰۰٪ چک
• تنظیم فرآیند
• ۵ نمونه متوالی را بررسی کنید
• ادامه روند
• اجرای ۷ نقطه به بالا یا پایین – دستورالعمل بالا

استفاده از نمودار

اگر فرآیند تحت کنترل باشد (و آمار فرآیند طبیعی باشد) ، ۹۹٫۷۳۰۰٪ از تمام نقاط بین محدوده کنترل قرار می گیرند. هرگونه مشاهدات خارج از محدوده ، یا الگوهای سیستماتیک در داخل ، نشان دهنده معرفی یک منبع جدید (و احتمالاً غیرقابل پیش بینی) از تنوع است که به عنوان تنوع علت خاص شناخته می شود. از آنجا که افزایش تنوع به معنای افزایش هزینه های کیفی است ، یک نمودار کنترلی “نشان دهنده” حضور علت خاصی است که نیاز به بررسی فوری دارد.

این باعث می شود محدودیت های کنترلی کمک های تصمیم گیری بسیار مهمی باشد. محدودیت های کنترل اطلاعاتی در مورد رفتار فرآیند ارائه می دهد و هیچ رابطه ذاتی با اهداف مشخصه یا تحمل مهندسی ندارد. در عمل ، میانگین فرایند (و از این رو خط مرکز) ممکن است با مقدار (یا هدف) مشخصه کیفیت مطابقت نداشته باشد زیرا طراحی فرایند به سادگی نمی تواند ویژگی فرایند را در سطح مورد نظر ارائه دهد.

نمودارهای کنترلی به دلیل تمایل افراد درگیر در فرایند (به عنوان مثال ، اپراتورهای ماشین) برای تمرکز بر انجام مشخصات ، در حالی که در واقع کم هزینه ترین روش این است که تنوع فرآیند را تا حد ممکن پایین نگه دارد ، محدودیت ها یا اهداف را محدود می کند. تلاش برای ایجاد فرایندی که مرکز طبیعی آن با هدف انجام شده یکسان نباشد تا مشخصات هدف را تغییر دهد و هزینه ها را به میزان قابل توجهی افزایش دهد و علت ناکارآمدی زیاد در عملیات باشد. با این حال ، مطالعات قابلیت پردازش رابطه بین محدودیت های طبیعی فرآیند (محدودیت های کنترل) و مشخصات را بررسی می کند.

هدف از افزودن محدودیت های هشدار یا تقسیم نمودار کنترل به مناطق ، ارائه اعلان اولیه در صورت خرابی است. به جای اینکه بلافاصله تلاش برای بهبود فرایند برای تعیین وجود علل خاص را آغاز کند ، مهندس کیفیت ممکن است سرعت برداشت نمونه ها را از خروجی فرایند به طور موقت افزایش دهد تا زمانی که مشخص شود که فرایند واقعاً تحت کنترل است. توجه داشته باشید که با محدودیت های سه سیگما ، تغییرات علت مشترک منجر به سیگنال های کمتر از یک بار از هر بیست و دو نقطه برای فرآیندهای کج و حدود یک بار از هر سیصد و هفتاد (۱/۳۷۰٫۴) امتیاز برای فرآیندهای معمولی توزیع شده می شود.

سطوح هشدار دو سیگما به ازای هر بیست و دو (۱/۹۸/۱/۹۸) نقطه رسم شده در داده های عادی توزیع شده تقریباً یک بار به دست می آید. (به عنوان مثال ، با توجه به قضیه محدودیت مرکزی ، میانگین نمونه های به اندازه کافی بزرگ که عملاً از هر توزیع زیرین که واریانس آن وجود دارد ، به طور معمول توزیع شده است.)

انتخاب محدودیت ها

شوارت بر اساس زیر محدودیت های ۳ سیگما (۳ انحراف معیار) را تعیین کرد.

نتیجه درشت نابرابری چبیشف که برای هر توزیع احتمالی ، احتمال خروجی بیشتر از k انحراف معیار از میانگین حداکثر ۱/k2 است.
نتیجه ظریف نابرابری ویسوچانسکی -پتونین ، که برای هر توزیع احتمالی یکنواخت ، احتمال نتیجه بیشتر از k انحراف استاندارد از میانگین حداکثر ۴/(۹k2) است.
در توزیع عادی ، یک توزیع احتمال بسیار رایج ، ۹۹٫۷ درصد از مشاهدات در سه انحراف استاندارد از میانگین (به توزیع عادی مراجعه کنید) انجام می شود.
شوهرت نتیجه گیری را خلاصه کرد و گفت:

… این واقعیت که معیاری که ما از آن استفاده می کنیم دارای اصل و نسب خوبی در قضایای آماری با ابروهای بالا است ، استفاده از آن را توجیه نمی کند. چنین توجیهی باید از شواهد تجربی مبنی بر م itثر بودن آن ناشی شود. همانطور که مهندس عملی می گوید ، اثبات پودینگ در خوردن است.

اگرچه او ابتدا محدودیت ها را بر اساس توزیع احتمال آزمایش کرد ، اما در نهایت شوارت نوشت:

برخی از اولین تلاش ها برای توصیف وضعیت کنترل آماری از این باور الهام گرفته شده بود که شکل خاصی از تابع فرکانس وجود دارد و اوایل استدلال شد که قانون عادی چنین وضعیتی را مشخص می کند. هنگامی که قانون عادی ناکافی تشخیص داده شد ، سپس اشکال کارکردی عمومی مورد آزمایش قرار گرفت. اما امروزه همه امیدها برای یافتن یک فرم کاربردی منحصر به فرد f بر باد رفته است.

نمودار کنترل به عنوان یک روش ابتکاری در نظر گرفته شده است. دمینگ اصرار داشت که این آزمون فرضیه نیست و انگیزه آن لمای نیمن -پیرسون نیست. او ادعا کرد که ماهیت ناهماهنگ جمعیت و چارچوب نمونه گیری در اکثر شرایط صنعتی استفاده از تکنیک های آماری متداول را به خطر انداخته است. قصد دمینگ این بود که در مورد سیستم علت یک فرایند  تحت طیف گسترده ای از شرایط ناشناخته ، آینده و گذشته [به نقل از منبع] وی ادعا کرد که در چنین شرایطی ، محدودیت های ۳ سیگما ارائه می شود. راهنمای منطقی و اقتصادی برای حداقل ضرر اقتصادی از دو خطا:

زمانی که در واقع علت متعلق به سیستم است (علت مشترک) ، یک تنوع یا یک اشتباه را به علت خاصی (علت قابل تعیین) نسبت دهید. (همچنین به عنوان خطای نوع I یا مثبت کاذب شناخته می شود)
تنوع یا اشتباهی را به سیستم نسبت دهید (علل رایج) در حالی که در واقع علت علت خاصی بوده است (علت قابل تعیین). (همچنین به عنوان خطای نوع II یا منفی کاذب شناخته می شود)

محاسبه انحراف معیار

در مورد محاسبه محدودیت های کنترل ، انحراف استاندارد (خطا) مورد نیاز از تغییرات متداول در فرآیند است. بنابراین ، برآورد کننده معمول ، از نظر واریانس نمونه ، مورد استفاده قرار نمی گیرد زیرا این مقدار کل خطای مربعی را از دلایل متداول و خاص تغییرات برآورد می کند.

یک روش جایگزین استفاده از رابطه بین محدوده نمونه و انحراف استاندارد آن است که توسط لئونارد اچ سی تیپت به دست آمده است ، به عنوان برآورد کننده که کمتر تحت تأثیر مشاهدات افراطی قرار می گیرد.

قوانین تشخیص سیگنال ها
متداول ترین مجموعه ها عبارتند از:

وسترن الکتریک قوانین خود را اعلام می کند
قوانین ویلر (معادل آزمایشات منطقه برق غربی)
نلسون قوانین را رعایت می کند
در مورد این که چه مدت یک دوره مشاهدات ، همه در یک سمت خط مرکزی ، باید به عنوان یک سیگنال در نظر گرفته شود ، ۶ ، ۷ ، ۸ و ۹ همه توسط نویسندگان مختلف حمایت می شوند.

مهمترین اصل برای انتخاب مجموعه ای از قوانین این است که انتخاب قبل از بازرسی داده ها انجام شود. انتخاب قوانین پس از مشاهده داده ها ، به دلیل اثرات آزمایش ارائه شده توسط داده ها ، میزان خطای نوع I را افزایش می دهد.

پایه های جایگزین

در سال ۱۹۳۵ ، موسسه استاندارد بریتانیا ، تحت تأثیر ایگون پیرسون و بر خلاف روح شوارت ، نمودارهای کنترلی را تصویب کرد و محدوده های ۳ سیگما را با محدودیت های بر اساس صدک های توزیع عادی جایگزین کرد. این حرکت همچنان توسط جان اوکلند و دیگران نمایندگی می شود ، اما به طور گسترده توسط نویسندگان در سنت شوارت -دمینگ مورد تحقیر قرار گرفته است.

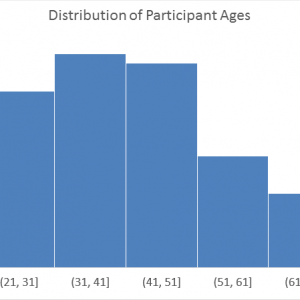
Histogram

هیستوگرام نمایشی تقریبی از توزیع داده های عددی است. اولین بار توسط کارل پیرسون معرفی شد. برای ساخت یک هیستوگرام ، اولین قدم این است که محدوده مقادیر را “bin” (یا “سطل” کنید – یعنی کل دامنه مقادیر را به یک سری فواصل تقسیم کنید – و سپس تعداد مقادیر را در هر بازه شمارش کنید. سطل های زباله معمولاً به عنوان فواصل متوالی و غیر همپوشانی یک متغیر مشخص می شوند. سطل زباله ها (فواصل) باید در مجاورت یکدیگر باشند و اغلب (اما لازم نیست که باشند) اندازه یکسانی دارند.

اگر سطل زباله ها مساوی باشد ، مستطیلی بر روی سطل با ارتفاع متناسب با فرکانس – تعداد موارد در هر سطل – نصب می شود. ممکن است هیستوگرام برای نمایش فرکانس های “نسبی” نرمال شود. سپس نسبت مواردی را که در هر یک از چند دسته قرار می گیرند ، نشان می دهد که مجموع ارتفاعات برابر ۱ است.

با این حال ، لازم نیست که سطل ها دارای عرض یکسان باشند. در این حالت ، مستطیل ساخته شده به گونه ای تعریف می شود که مساحت آن متناسب با فراوانی موارد موجود در سطل زباله باشد. بنابراین محور عمودی فرکانس نیست بلکه چگالی فرکانس است – تعداد موارد در واحد متغیر در محور افقی. نمونه هایی از عرض سطل متغیر در داده های دفتر سرشماری در زیر نشان داده شده است.

با توجه به اینکه سطل های مجاور هیچ شکافی باقی نمی گذارند ، مستطیل های هیستوگرام یکدیگر را لمس می کنند تا نشان دهد که متغیر اصلی پیوسته است.

هیستوگرام ها به طور تقریبی از چگالی توزیع زیرین داده ها و اغلب برای تخمین چگالی استفاده می کنند: برآورد تابع چگالی احتمال متغیر زیرین. مساحت کل هیستوگرام مورد استفاده برای چگالی احتمال همیشه به ۱ عادی می شود. اگر طول فواصل در محور x همه ۱ باشد ، هیستوگرام با نمودار فرکانس نسبی یکسان است.

هیستوگرام را می توان یک تخمین ساده چگالی هسته در نظر گرفت ، که از هسته برای صاف کردن فرکانس ها بر روی سطل ها استفاده می کند. این یک تابع چگالی احتمال نرم تر را ارائه می دهد ، که به طور کلی توزیع متغیر زیر را با دقت بیشتری نشان می دهد. برآورد چگالی را می توان به عنوان جایگزینی برای هیستوگرام ترسیم کرد و معمولاً به عنوان یک منحنی و نه مجموعه ای از جعبه ها ترسیم می شود. با وجود این ، هیستوگرام ها در برنامه های کاربردی ترجیح داده می شوند ، هنگامی که ویژگی های آماری آنها نیاز به مدل سازی دارد. توصیف تغییرات چگالی هسته از نظر ریاضی بسیار دشوار است ، در حالی که برای هیستوگرام که هر سطل به طور مستقل متفاوت است ساده است.

جایگزینی برای تخمین چگالی هسته ، میانگین هیستوگرام جابجا شده است ،که سریع محاسبه می شود و برآورد منحنی صافی از چگالی را بدون استفاده از هسته ارائه می دهد.
هیستوگرام یکی از هفت ابزار اصلی کنترل کیفیت است.

هیستوگرام ها گاهی با نمودارهای میله اشتباه گرفته می شوند. یک هیستوگرام برای داده های پیوسته استفاده می شود ، جایی که سطل ها محدوده داده را نشان می دهند ، در حالی که نمودار میله نمودار متغیرهای طبقه ای است. برخی از نویسندگان توصیه می کنند که نمودارهای میله ای برای روشن شدن تمایز بین مستطیل ها فاصله داشته باشند.

تعاریف ریاضی

داده های مورد استفاده برای ساخت هیستوگرام از طریق یک تابع mi تولید می شود که تعداد مشاهداتی را که در هر یک از دسته های جدا از هم قرار می گیرند شمارش می کند (معروف به سطل). بنابراین ، اگر n تعداد کل مشاهدات و k کل تعداد سطل ها باشد ، داده های هیستوگرام mi شرایط زیر را برآورده می کند:

{\ displaystyle n = \ sum _ {i = 1}^{k} {m_ {i}}.} n = \ sum_ {i = 1}^k {m_i}.
هیستوگرام تجمعی
هیستوگرام تجمعی نگاشتی است که تعداد تجمعی مشاهدات را در همه سطل ها تا سطل مشخص شده شمارش می کند. یعنی هیستوگرام تجمعی Mi یک هیستوگرام mj به صورت زیر تعریف می شود:

{\ displaystyle M_ {i} = \ sum _ {j = 1}^{i} {m_ {j}}.} M_i = \ sum_ {j = 1}^i {m_j}.
تعداد سطل و عرض
هیچ “بهترین” تعداد سطل زباله وجود ندارد و اندازه های مختلف سطل زباله می تواند ویژگی های مختلف داده ها را نشان دهد. داده های گروه بندی حداقل به اندازه آثار گرانت در قرن ۱۷ قدمت دارد ، اما هیچ راهنمای سیستماتیک [۱۱] تا کار استرجس در سال ۱۹۲۶ ارائه نشد.

استفاده از سطل های وسیع تر که در آن تراکم نقاط داده زیرین کم است ، به دلیل تصادفی بودن نمونه ، نویز را کاهش می دهد. استفاده از سطل های باریک در جایی که چگالی زیاد است (بنابراین سیگنال باعث کاهش نویز می شود) دقت بیشتری در برآورد چگالی می دهد. بنابراین تغییر عرض بن در یک هیستوگرام می تواند مفید باشد. با این وجود ، سطل های با عرض مساوی بسیار مورد استفاده قرار می گیرند.

برخی از نظریه پردازان سعی کرده اند تعداد مطلوبی از سطل ها را تعیین کنند ، اما این روش ها به طور کلی مفروضات قوی در مورد شکل توزیع ارائه می دهند. بسته به توزیع واقعی داده ها و اهداف تجزیه و تحلیل ، ممکن است عرض های مختلف سطل مناسب باشد ، بنابراین برای تعیین عرض مناسب معمولاً آزمایش لازم است. با این حال ، دستورالعمل ها و قوانین مختلف مفیدی وجود دارد.

تعداد سطل k را می توان مستقیماً اختصاص داد یا می توان از عرض سطل پیشنهادی h به صورت زیر محاسبه کرد.

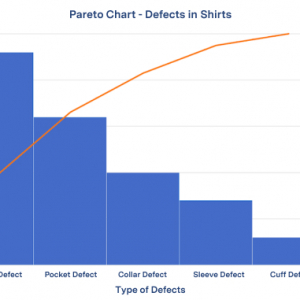
Pareto chart

نمودار پارتو یک نوع نمودار است که هم میله ها و هم نمودار خطی را شامل می شود ، که در آن مقادیر جداگانه به ترتیب نزولی توسط میله ها نشان داده می شود و مجموع تجمعی با خط نشان داده می شود. این نمودار بر اساس اصل پارتو نامگذاری شده است که به نوبه خود نام خود را از ویلفردو پارتو ، اقتصاددان مشهور ایتالیایی گرفته است.

محور عمودی سمت چپ فراوانی وقوع است ، اما می تواند هزینه یا واحد اندازه گیری مهم دیگری را نشان دهد. محور عمودی راست درصد تجمعی تعداد کل وقایع ، هزینه کل یا کل واحد اندازه گیری خاص است. از آنجا که مقادیر در حال کاهش هستند ، تابع تجمعی یک تابع مقعر است. برای مثال زیر ، برای کاهش ۷۸ درصدی میزان دیررس ، کافی است سه مورد اول را حل کنید.

هدف از نمودار پارتو برجسته سازی مهمترین آنها در بین عوامل (معمولاً بزرگ) است. در کنترل کیفیت ، نمودارهای پارتو برای یافتن عیب هایی که باید در اولویت قرار گیرند تا بیشترین بهبود کلی را مشاهده کنند ، مفید است. اغلب نشان دهنده رایج ترین منابع نقص ، بیشترین نوع نقص ، یا شایع ترین دلایل شکایت مشتری و غیره است. ویلکینسون (۲۰۰۶) الگوریتمی برای تولید محدودیت های پذیرش مبتنی بر آماری (مشابه فواصل اطمینان) برای هر نوار در نمودار پارتو ابداع کرد.

این نمودارها را می توان با برنامه های صفحه گسترده ساده ، ابزارهای نرم افزاری آماری تخصصی و تولیدکنندگان نمودارهای کیفیت آنلاین تولید کرد.

نمودار پارتو یکی از هفت ابزار اساسی کنترل کیفیت است.

Scatter plot

نمودار پراکندگی (که پراکندگی ، نمودار پراکندگی ، نمودار پراکندگی ، پراکندگی یا نمودار پراکندگی نیز نامیده می شود) نوعی نمودار یا نمودار ریاضی است که از مختصات دکارتی برای نمایش مقادیر معمولاً دو متغیر برای مجموعه ای از داده ها استفاده می کند. اگر نقاط کد شده (رنگ/شکل/اندازه) ، یک متغیر اضافی می تواند نمایش داده شود. داده ها به صورت مجموعه ای از نقاط نمایش داده می شوند که هر یک دارای مقدار یک متغیر است که موقعیت را در محور افقی تعیین می کند و مقدار متغیر دیگر موقعیت را در محور عمودی تعیین می کند.

بررسی اجمالی

زمانی که یک متغیر پیوسته تحت کنترل آزمایشگر است و دیگری به آن بستگی دارد یا زمانی که هر دو متغیر پیوسته مستقل هستند ، می توان از نمودار پراکندگی استفاده کرد. اگر پارامتری وجود داشته باشد که به طور سیستماتیک توسط دیگری افزایش یا کاهش می یابد ، آن را پارامتر کنترل یا متغیر مستقل می نامند و معمولاً در امتداد محور افقی رسم می شود. متغیر اندازه گیری شده یا وابسته معمولاً در امتداد محور عمودی رسم می شود. در صورت عدم وجود متغیر وابسته ، هر دو نوع متغیر را می توان در هر محور رسم کرد و نمودار پراکندگی تنها میزان همبستگی (و نه علیت) بین دو متغیر را نشان می دهد.

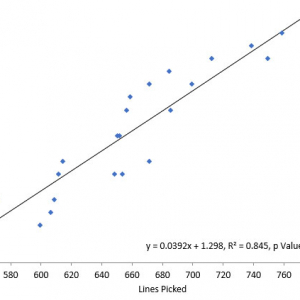
یک نمودار پراکندگی می تواند انواع مختلفی از همبستگی بین متغیرها را با فاصله اطمینان مشخص نشان دهد. به عنوان مثال ، وزن و ارتفاع در محور y و ارتفاع در محور x خواهد بود. همبستگی ها ممکن است مثبت (صعودی) ، منفی (سقوط) ، یا صفر (غیر مرتبط) باشد. اگر الگوی نقطه ها از سمت چپ پایین به راست بالا نشان دهنده همبستگی مثبت بین متغیرهای مورد مطالعه است. اگر الگوی نقاط از بالا سمت چپ به پایین راست شیب داشته باشد ، نشان دهنده همبستگی منفی است. برای مطالعه رابطه بین متغیرها ، می توان خطی از بهترین تناسب (که خط متداول نامیده می شود) ترسیم کرد.

یک معادله برای همبستگی بین متغیرها را می توان با روشهای مناسب ترین تعیین کرد. برای یک همبستگی خطی ، بهترین روش به عنوان رگرسیون خطی شناخته می شود و تضمین می شود که یک راه حل صحیح را در یک زمان محدود تولید کند. هیچ روشی که بهترین تناسب جهانی را داشته باشد تضمین نمی کند که یک راه حل مناسب برای روابط دلخواه ایجاد کند. یک نمودار پراکندگی نیز زمانی مفید است که بخواهیم ببینیم چگونه دو مجموعه داده قابل مقایسه برای نشان دادن روابط غیر خطی بین متغیرها توافق می کنند. توانایی انجام این کار را می توان با افزودن یک خط صاف مانند LOESS افزایش داد. علاوه بر این ، اگر داده ها با یک مدل ترکیبی از روابط ساده نشان داده شوند ، این روابط از نظر بصری به عنوان الگوهای اضافه شده آشکار خواهند بود.

نمودار پراکندگی یکی از هفت ابزار اساسی کنترل کیفیت است.

نمودارهای پراکندگی را می توان در قالب نمودارهای حبابی ، نشانگر یا/و خطی ساخت.

مثال : به عنوان مثال ، برای نشان دادن ارتباط بین ظرفیت ریه فرد و مدت زمانی که فرد می تواند نفس خود را نگه دارد ، یک محقق گروهی از افراد را برای مطالعه انتخاب می کند ، سپس ظرفیت ریه هر فرد (اولین متغیر) و مدت زمان آن فرد را اندازه گیری می کند. نفس خود را نگه دارند (متغیر دوم). سپس محقق داده ها را در یک نمودار پراکنده ترسیم می کند و “ظرفیت ریه” را به محور افقی و “زمان حبس نفس” را به محور عمودی اختصاص می دهد.

فردی با ظرفیت ریه ۴۰۰ cl که نفس خود را برای ۲۱٫۷ ثانیه نگه داشته است ، با یک نقطه در نمودار پراکندگی در نقطه (۴۰۰ ، ۲۱٫۷) در مختصات دکارتی نشان داده می شود. طرح پراکندگی همه افراد در مطالعه محقق را قادر می سازد تا مقایسه بصری دو متغیر در مجموعه داده ها را بدست آورد و به تعیین نوع رابطه بین این دو متغیر کمک می کند.

ماتریس های نمودار پراکنده

برای مجموعه ای از متغیرهای داده (ابعاد) X1 ، X2 ، … ، Xk ، ماتریس نمودار پراکندگی تمام نمودارهای پراکندگی زوجی متغیرها را در یک نمای واحد با چندین پراکندگی در قالب ماتریس نشان می دهد. برای متغیرهای k ، ماتریس scatterplot شامل k سطر و k ستون خواهد بود. نمودار واقع در محل تلاقی سطر و ستون jth ، نمودار متغیرهای Xi در مقابل Xj است.این بدان معناست که هر سطر و ستون یک بعد هستند و هر سلول یک نمودار پراکندگی دو بعدی را ترسیم می کند.

یک ماتریس طرح پراکندگی عمومی طیف وسیعی از نمایش ترکیبات زوجی متغیرهای دسته ای و کمی را ارائه می دهد. برای نمایش دو متغیر طبقه ای می توان از نمودار موزاییک ، نمودار نوسان یا نمودار میله ای وجهی استفاده کرد. نمودارهای دیگر برای یک متغیر طبقه ای و یک متغیر کمی استفاده می شود.

Stratified sampling

در آمارگیری ، نمونه گیری طبقه ای روشی برای نمونه گیری از جمعیت است که می تواند به زیرجمعیت ها تقسیم شود.

در نظرسنجی های آماری ، هنگامی که زیرجمعیت ها در کل جمعیت متفاوت است ، می توان به طور مستقل از هر زیرجمعیت (قشر) نمونه گرفت. طبقه بندی فرایند تقسیم اعضای جمعیت به زیر گروههای همگن قبل از نمونه گیری است.

اقشار باید قسمتی از جمعیت را تعریف کنند. یعنی باید به طور جمعی جامع و متقابلاً متقابل باشد: هر عنصر در جمعیت باید به یک و تنها یک قشر اختصاص داده شود. سپس نمونه گیری تصادفی ساده در داخل هر قشر اعمال می شود. هدف بهبود دقت نمونه با کاهش خطای نمونه برداری است. این می تواند میانگین وزنی تولید کند که دارای تنوع کمتری نسبت به میانگین حسابی یک نمونه تصادفی ساده از جمعیت است.

در آمارهای محاسباتی ، نمونه گیری طبقه ای روشی برای کاهش واریانس است که از روش های مونت کارلو برای تخمین آمار جمعیت از یک جمعیت شناخته شده استفاده می شود.

مثال : فرض کنید ما باید میانگین تعداد آرا را برای هر نامزد در یک انتخابات برآورد کنیم. فرض کنید یک کشور دارای ۳ شهر است: شهر A دارای ۱ میلیون کارگر کارخانه ، شهر B دارای ۲ میلیون کارمند اداری و شهر C 3 میلیون بازنشسته دارد. ما می توانیم یک نمونه تصادفی با اندازه ۶۰ را برای کل جمعیت دریافت کنیم ، اما برخی احتمال وجود دارد که نمونه تصادفی حاصله در این شهرها ضعیف باشد و از این رو مغرضانه باشد ، و باعث ایجاد خطای قابل توجهی در برآورد شود (هنگامی که نتیجه مورد نظر توزیع متفاوت ، از نظر پارامتر مورد علاقه ، بین شهرها). در عوض اگر ما یک نمونه تصادفی ۱۰ ، ۲۰ و ۳۰ را به ترتیب از شهرهای A ، B و C انتخاب کنیم ، می توانیم خطای کوچکتری در برآورد اندازه کل نمونه مشابه ایجاد کنیم. این روش عموماً زمانی مورد استفاده قرار می گیرد که جمعیت یک گروه همگن نباشد.

استراتژی های نمونه گیری طبقه ای

در تخصیص متناسب از بخش نمونه برداری در هر یک از اقشار متناسب با کل جمعیت استفاده می شود. به عنوان مثال ، اگر جمعیت شامل n نفر باشد که m از آنها مرد و f زن هستند (و m + f = n) ، اندازه نسبی دو نمونه (x1 = m/n مرد ، x2 = f/ n زن) باید این نسبت را منعکس کند.
تخصیص بهینه (یا تخصیص نامتناسب) – بخش نمونه برداری از هر قشر متناسب با نسبت (همانطور که در بالا گفته شد) و انحراف استاندارد توزیع متغیر است. نمونه های بزرگتری در اقشار با بیشترین تنوع گرفته می شود تا کمترین واریانس کلی نمونه ممکن را ایجاد کند.
نمونه واقعی استفاده از نمونه گیری طبقه ای برای یک نظرسنجی سیاسی خواهد بود. اگر پاسخ دهندگان نیاز به نشان دادن تنوع جمعیت داشته باشند ، محقق به طور خاص به دنبال مشارکت شرکت کنندگان در گروه های مختلف اقلیت مانند نژاد یا مذهب بر اساس تناسب آنها با کل جمعیت است که در بالا ذکر شد. بنابراین یک نظرخواهی طبقه ای می تواند ادعا کند که بیشتر از یک نمونه گیری تصادفی ساده یا نمونه گیری سیستماتیک نماینده جمعیت است.

مزایای

دلایل استفاده از نمونه گیری طبقه ای به جای نمونه گیری تصادفی ساده شامل

اگر اندازه گیری ها در داخل اقشار دارای انحراف معیار کمتری باشند (در مقایسه با انحراف استاندارد کلی در جمعیت) ، طبقه بندی خطای کوچکتری در برآورد ایجاد می کند.
برای بسیاری از برنامه های کاربردی ، اندازه گیری ها زمانی کنترل می شوند و/یا ارزان تر می شوند که جمعیت در اقشار گروه بندی شوند.
وقتی مطلوب است که برآورد پارامترهای جمعیت برای گروه های درون جمعیت وجود داشته باشد – نمونه گیری طبقه ای تأیید می کند که ما نمونه های کافی از اقشار مورد نظر داریم.
اگر تراکم جمعیت در یک منطقه بسیار متغیر باشد ، نمونه گیری طبقه ای تضمین می کند که می توان برآوردها را با دقت مساوی در نقاط مختلف منطقه انجام داد و مقایسه مناطق فرعی را می توان با قدرت آماری برابر انجام داد. به عنوان مثال ، در انتاریو در نظرسنجی انجام شده در سراسر استان ممکن است از بخش نمونه برداری بزرگتر در مناطق کم جمعیت شمال استفاده شود ، زیرا اختلاف جمعیت بین شمال و جنوب به حدی زیاد است که کسر نمونه بر اساس نمونه استان به طور کلی ممکن است منجر به جمع آوری تنها تعداد انگشت شماری از داده های شمال.

معایب

نمونه گیری طبقه ای زمانی مفید نیست که جمعیت را نتوان به طور کامل به زیر گروههای جدا از هم تقسیم کرد. این یک روش نادرست برای ایجاد اندازه نمونه های زیر گروه ها با میزان داده های موجود از زیر گروه ها است ، نه اینکه اندازه نمونه ها را به اندازه زیرگروه ها (یا با تفاوت های آنها ، در صورتی که تفاوت قابل ملاحظه ای نشان می دهد – به عنوان مثال با استفاده از تست F) اگر مشکوک به تغییرات در بین آنها نمونه گیری طبقه ای باشد ، داده هایی که هر زیر گروه را نشان می دهند دارای اهمیت یکسانی هستند. اگر واریانس های زیرگروه به طور قابل توجهی متفاوت باشند و داده ها نیاز به طبقه بندی با واریانس داشته باشند ، نمی توان به طور همزمان اندازه هر نمونه زیر گروه را متناسب با اندازه زیر گروه در کل جمعیت دانست.

برای روشی کارآمد برای تقسیم منابع نمونه گیری در بین گروه هایی که از نظر وسعت ، واریانس و هزینه متفاوت هستند ، به “تخصیص بهینه” مراجعه کنید. مشکل نمونه گیری طبقه ای در مورد طبقه قبلی ناشناخته (نسبت زیرجمعیت ها در کل جمعیت) می تواند تأثیر مخربی بر عملکرد هرگونه تجزیه و تحلیل بر روی مجموعه داده داشته باشد ، به عنوان مثال. طبقه بندی.در این راستا ، می توان از نمونه گیری مینیماکس برای قوی سازی مجموعه داده با توجه به عدم قطعیت در فرایند تولید داده های اساسی استفاده کرد.

ترکیب زیر لایه ها برای اطمینان از تعداد کافی می تواند منجر به پارادوکس سیمپسون شود ، جایی که روندهایی که در واقع در گروه های مختلف داده وجود دارد ، ناپدید می شوند یا حتی با ترکیب گروه ها معکوس می شوند.

تخصیص اندازه نمونه

برای استراتژی تخصیص متناسب ، اندازه نمونه در هر قشر متناسب با اندازه قشر گرفته می شود. فرض کنید در یک شرکت پرسنل زیر وجود دارد:

مرد ، تمام وقت: ۹۰
مرد ، پاره وقت: ۱۸
زن ، تمام وقت: ۹
زن ، پاره وقت: ۶۳
مجموع: ۱۸۰
و از ما خواسته می شود که نمونه ای از ۴۰ نفر از کارکنان را که طبق طبقه بندی های بالا طبقه بندی شده اند ، انتخاب کنیم.

اولین قدم محاسبه درصد هر گروه از کل است.

٪ مرد ، تمام وقت = ۹۰ ÷ ۱۸۰ = ۵۰٪
٪ مرد ، پاره وقت = ۱۸ ÷ ۱۸۰ = ۱۰٪
٪ زن ، تمام وقت = ۹ ÷ ۱۸۰ = ۵٪
٪ زن ، پاره وقت = ۶۳ ÷ ۱۸۰ = ۳۵٪

این به ما می گوید که از نمونه ۴۰ ما ،

۵۰٪ (۲۰ نفر) باید مرد و تمام وقت باشند.
۱۰٪ (۴ نفر) باید مرد و پاره وقت باشند.
۵ ((۲ نفر) باید زن و تمام وقت باشند.
۳۵٪ (۱۴ نفر) باید زن باشند ، به صورت پاره وقت.

یک راه آسان دیگر بدون نیاز به محاسبه درصد این است که اندازه هر گروه را در اندازه نمونه ضرب کرده و بر تعداد کل جمعیت (اندازه کل کارکنان) تقسیم کنید:

مرد ، تمام وقت = ۹۰ × (۱۸۰ ۴۰ ۴۰) = ۲۰
مرد ، نیمه وقت = ۱۸ × (۱۸۰ ۴۰ ۴۰) = ۴
زن ، تمام وقت = ۹ × (۱۸۰ ۴۰ ۴۰) = ۲
زن ، پاره وقت = ۶۳ × (۱۸۰ ۴۰ ۴۰) = ۱۴

هدف از نمودارهای کنترلی این است که اجازه دهیم رویدادهایی را که نشان دهنده تغییرات واقعی فرآیند هستند ، تشخیص دهیم. این تصمیم ساده در مواردی که ویژگی فرایند به طور مداوم متغیر است ، می تواند مشکل باشد. نمودار کنترل معیارهای عینی تغییر را ارائه می دهد. هنگامی که تغییر تشخیص داده می شود و خوب تلقی می شود ، باید علت آن شناسایی شود و احتمالاً به شیوه جدیدی از کار تبدیل شود ، در صورتی که تغییر بد باشد ، باید علت آن شناسایی و حذف شود.

جهت مطالعه موارد مرتبط با علوم کامپیوتر و الکترونیک:

• نرم افزار ها
• سخت افزار ها
• رباتیک
• هوش مصنوعی
• گیربکس و طراحی آن
• معاملات خودرو در علم اقتصاد
• آشنایی با هوافضا
• برق و الکترونیک در علوم مهندسی